Calculating the force and kinetic coefficient of friction
The tables on this page are based on calculations by Dr. Heribert Illig and Prof. Dr. Dipl. Ing. H.U. Niemitz [1].
The results in a nutshell - Factors for calculating - Friction and coefficient of friction - Friction and lubrication - Force exerted by each hauler - Force on inclined plane, no rope roll - Force dependent on friction - Force dependent on adhesion - Including weight and gravity - Calculating haulers with / without rope roll - Checking with more friction - Checking with more extended force - Conclusions - Heavy granite blocks - Sources
 The results in a nutshell
The results in a nutshell
With the following calculations [1] we provide
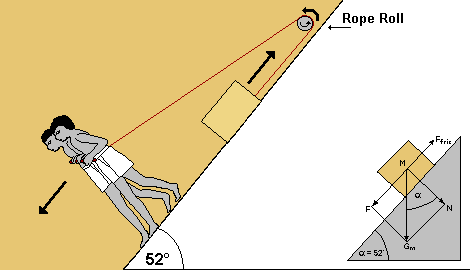
evidence, that with the help of the rope roll it is possible to haul a
2.5 tons stone block including sledge up the 52° incline of the flank
of the pyramid. The rope roll redirects the force needed, so you need
only 46 haulers and they are actually walking down the slope, thus using
their own weight in addition to their strength to pull the stone.
![]() Löhner's rope roll
Löhner's rope roll
Thanks to the rope roll the transport of a 2.5 tons stone block can be accomplished on the 52° flank of the pyramid with only 46 haulers. |
For the pyramid of Khufu we compute the following numbers per team (= hauling team for one 2.5 tons stone block):
| Pyramid flank (52°): we get a hauling team of 55 men on the pyramid flank. The number of 46 haulers is rounded up to 48 men, because they work in 2 groups and in pairs of 2 men each. We add 7 men - an overseer, lubricator and men for checking the tracks and the ropes, stopping the stones from sliding down the tracks and for working at the rope roll station. Gradient of 5°: For the causeway we need 23 haulers. This number is rounded to 24 men, because they work in 2 groups and in pairs of 2 men each. Together with 2 men in reserve and 4 additional workers we get a hauling team of 30 men. On level surface: here 11 haulers are enough. This number is rounded to 12, because they work in 2 groups and in pairs of 2 men each. Including a overseer, and some men to take care of the tracks and ropes we get a hauling team of 15 men. |
![]() Detailed calculations how many workers
were necessary to build the pyramid
Detailed calculations how many workers
were necessary to build the pyramid
Can this model also be used for hauling the 40 to 50 tons granite blocks
required for the King's chamber up the pyramid?
![]() Transporting the large granite blocks
up the pyramid
Transporting the large granite blocks
up the pyramid
 What factors have to be taken in account in calculating the force required?
What factors have to be taken in account in calculating the force required?
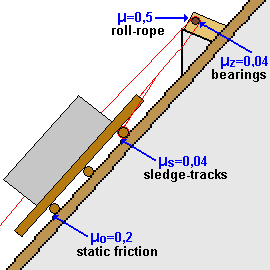 |
1. The friction between the sledge and the tracks μs
(reduced by using a lubricant) 2. The friction between the bearing of the rope roll and the wooden crossbeam of the rope roll μz (reduced by using a lubricant) 3. The tractive force of the haulers on level ground 4. The angle of inclination (52° = flank of the pyramid of Khufu ) 5. The weight of the haulers and the influence of the gravitational force when using Franz Löhner's rope roll 6. Static friction μo between sledge and tracks |
 What is friction and what is a coefficient of friction
What is friction and what is a coefficient of friction
The resistance to lateral motion when one attempts to slide the surface of one object over another surface is called friction or traction. Depending on the type of materials that are in contact, the force one needs to overcome friction can vary. To overcome or lower friction / traction a lubricant is used.
The coefficient of friction is a value which describes the ratio of the force of friction between two bodies and the force pressing them together. The coefficient of friction depends on the materials used and if the bodies are moving or not [4].
 Friction and lubrication
Friction and lubrication
Friction of the rope:
The revolving rope should have as little stiction [4]
and slack as possible and not slip over the wood. That is to say the difference
between the rotational speed of the rope and the speed of the wood should
be as small as possible. The coefficient of friction of hemp rope on rough
wood is μ=0,5. That is very high, which means, that the rope will
only be rubbing slightly on the wood.
![]() Löhner's rope roll
Löhner's rope roll
Kinetic (or dynamic) friction of the rope roll:
The kinetic friction of the rope roll is very important. You
can lower it by choosing which materials you are using.
| Coefficient of kinetic friction μ [2] | dry | lubricated |
on this page |
| Wood on wood | 0,2 - 0,4 | 0,04 - 0,16 | |
| Wood on metal | 0,2 - 0,5 | 0,02 - 0,1 | 0,04 |
| Metal on metal | 0,1 - 0,25 | 0,01 - 0,15 |
These numbers are not the same as for static friction - those are higher.
For example for wood on wood the static friction is 0,40 to 0,75 (dry)!
![]() Löhner's rope roll
Löhner's rope roll
Lubricating medium:
A common way to lessen the coefficient of friction and thus to
reduce friction is by using a lubricant that is placed between the two
surfaces. Of course the addition of a lubricant also has a significant
effect on reducing the required hauling force. Through practical application
the ancient Egyptians must have been able to lower the friction between
the materials they used to a value in the lower scope of the scale.
We use the lower values for calculating:
- Coefficient of friction between sledge and track μs
= 0,04
- Coefficient of friction between wooden and metal bearing of the rope
roll μz = 0,04
1. Lubricating the interface between the tracks and the sledge
assembly:
Franz Löhner did some trials and had the best results with slightly
watered oil.
![]() Using lubricants for wooden sledges
Using lubricants for wooden sledges
2. Lubricating the bearing of the rope roll:
Oil is better than animal fat. Possibly the Egyptians even used so called
copper grease, a product made from finely grinded copper and oil.
![]() Löhner's rope roll (more information)
Löhner's rope roll (more information)
 Force exerted by each hauler
Force exerted by each hauler
We think, that each hauler was capable of developing a force of 12 kp (= 117.7N / 1kp = 9,80665 g·m/s²).
This value once was used to calculate the force exerted by one worker when towing barges on the French canals. This value was also used by Goyon for his calculations [3]. Various publications use values of 10 to 15 kp (see calculations with 15kp instead of 12kp). We use the lower values and see if it still works.
Towing and hauling both demand a continuous effort over a long period of time. That is why this value is noticeable lower than the maximum force a human being can apply. The process of hauling should be interrupted as little as possible, because every time you have to start moving the sledge again, you have to overcome static friction (stiction [4]).
For this reason, the haulers should be able to walk at a normal pace (= walking 20m per minute) and continuously without stopping until the next team takes over from them for the next leg. The hand off to the next hauling team should be accomplished in such a way, that the sledge doesn't stop its movement.
For checking purposes:
On the well known wall painting in the tomb of Djehutiotep at
Deir El Bersheh (El Bersha) 172 haulers are depicted pulling a colossal
statue, weighting about 58 to 60 tons on a sledge (Illustration).
If we take 12kp for each man, then the 172 haulers will exert 2'064 kp.
As a coefficient of friction μs we
calculate 0,0344 (2'064 : 60'000 = 0,0344). For our calculations on this
page we increase it to 0,04 (see further up).
![]() Sledge for transporting the stone
blocks: Illustration of the wall painting in the tomb of Djehutiotep
Sledge for transporting the stone
blocks: Illustration of the wall painting in the tomb of Djehutiotep
| F = Gm· μs |
F = Force / Gm = Weight / μs = Coefficient of friction (between sledge and tracks)
 Force on an inclined plane without a rope roll
Force on an inclined plane without a rope roll
A ramp is an inclined plane. By changing the angle of the ramp, the force necessary to raise or lower a load is varied.
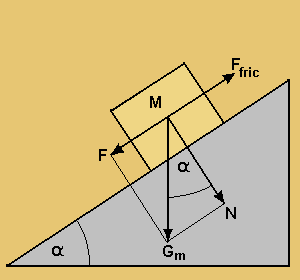
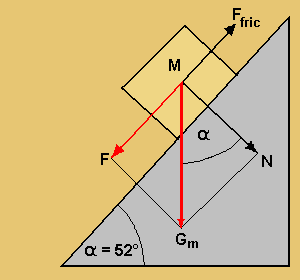
F = Force (downhill-slope force)
Ffric = Frictional force of the inclined
plane / N = Normal force that is perpendicular to the
plane / Gm = force of gravity on the object
(= weight) / α = Angle of inclination
If we increase the angle of inclination of the plane (right), the stone will start to slide down faster.
As you know from your own experience the steeper a slope, the greater will be your effort to push or haul a load upwards. As we will see further on, at a certain point the angle of inclination is so large, that a stone block will start sliding down. But if we use a rope roll to help, this will happen much later and at a much steeper angle.
Without employing a rope roll we use the following equation:
F = Gm· (sin α + μs · cos α) |
F = Force / Gm = Weight / μs = Coefficient of friction (between sledge and tracks) / α = Angle of inclination
 Force dependent on friction
Force dependent on friction
Now the coefficient of friction of the bearing of the rope roll μz
has to be included in the equation. If this coefficient increases, the
force needed becomes distinctly higher (see last column of chart 1).
F = Force / Gm = Weight
/ μs = Coefficient of friction (between
sledge and tracks) / μz = Coefficient
of static friction (between bearings and roll) / α
= Angle of inclination
F= |
Gm·
(sin α + μs · cos α) · (1 + μz) ---------------------------------- (1 -μz) |
We use the following values for calculating:
1. Coefficient of friction between sledge and tracks μs
= 0,04 (see lubricating medium)
2. Coefficient of friction of the bearing of the rope roll μz
= 0,00 to 0,6 (using lubricants this value can possibly be lowered to
μz = 0,04)
3. Angle of inclination α = 0° to 52° (= angle of inclination
of the flank of the pyramid of Khufu)
4. Weight of one stone block (2.500 kg) plus sledge, rope and harness
(300 kg) = 2800 kg [5]
CHART 1 (figures [1] page 76)
| μz | 0,00 |
0,03 |
0,04 |
0,05 |
0,10 |
0,50 |
0,60 |
| α = 0° | 112 |
119 |
121 |
124 |
137 |
336 |
448 |
| α = 5° | 356 |
378 |
385 |
393 |
435 |
1067 |
1422 |
| α = 10° | 597 |
633 |
646 |
659 |
729 |
1789 |
2386 |
| α = 20° | 1063 |
1151 |
1151 |
1175 |
1299 |
3189 |
4252 |
| α = 30° | 1497 |
1622 |
1622 |
1654 |
1830 |
4491 |
5988 |
| α = 40° | 1886 |
2002 |
2043 |
2084 |
2305 |
5657 |
5742 |
| α = 52° | 2275 kp |
2416 kp |
2465 kp |
2515 kp |
2781 kp |
6826 kp |
9101 kp |
The value 0,00 (first column) shows which forces accrue without the rope roll. The value 0,04 (third column) assumes you are using the rope roll. The values of the third column are higher, because we haven't included the influence of weight and gravity yet (see further down).
 Force dependent on adhesion - at what point do you start slipping?
Force dependent on adhesion - at what point do you start slipping?
If the friction is smaller than the weight component along the plane, the block starts slipping and slides down with acceleration.
We now have to include the coefficient of static friction / adhesion
μo in our calculations. The force used depends on the
adhesion on the inclined plane. For a ramp we can use μo
= 0,2.
F = Force / Gm = Weight
/ μo = Coefficient of static friction
(between sledge and tracks) / α = Angle of inclination
F = Gm· ((μo · cos α) - sin α) |
If using Gm = 60kg as the weight of one hauler, the stone starts to slip at an angle of inclination of 20° and with better adhesion the stone starts slipping at 30° (Force = negative, shown on the chart as "-").
CHART 2 (figures [1] page 77)
| F with μo
= 0,2 |
F with μo
= 0,25 |
F with μo
= 0,4 |
F with μo
= 0,6 |
|
| α = 0° | 12,0 kp |
15,0 kp |
24,0 kp |
36,0 kp |
| α = 5° | 6,7 kp |
9,72 kp |
18,7 kp |
31,0 kp |
| α = 10° | 1,4 kp |
4.38 kp |
13,2 kp |
25,0 kp |
| α = 20° | - |
- |
2,0 kp |
13,3 kp |
| α = 30° | - |
- |
- |
1,2 kp |
| α = 40° | - |
- |
- |
- |
| α = 52° | - |
- |
- |
- |
Conclusion from chart 1 and 2: An inclination of 5° reduces the force of one hauler from 12 to 6,7 kp (= half / chart 2). At the same time the force, the hauling teams has to generate to haul the stone up the incline, increases from 112 to 356 kp (= 3 times / chart 1, first column). |
 Including the weight of the haulers and the influence of gravity
Including the weight of the haulers and the influence of gravity
The steeper the ramp becomes, the better the haulers can use their own weight (60 kg) as a load to counterbalance the stone being carried up.
F = Force / Gm = Weight / μo = Coefficient of static friction (between sledge and tracks) / α = Angle of inclination
F = Gm· ((μo · cos α) + sin α) |
CHART 3 (figures [1] page 80)
F with μo
= 0,2 |
F with μo
= 0,4 |
F with μo
= 0,6 |
|
| α = 0° | 12,0 kp |
24,0 kp |
36,0 kp |
| α = 5° | 17,2 kp |
29,1 kp |
41,1 kp |
| α = 10° | 22,2 kp |
34,0 kp |
45,9 kp |
| α = 20° | 31,8 kp |
43,1 kp |
54,3 kp |
| α = 30° | 40,4 kp |
50,8 kp |
61,2 kp |
| α = 40° | 47,8 kp |
57,0 kp |
66,2 kp |
| α = 52° | 54,7 kp |
62,1 kp |
69,4 kp |
| α = 60° | 58,0 kp | 64,0 kp | 70,0 kp |
| α = 70° | 60,5 kp | 64,6 kp | 68,7 kp |
| α = 80° | 61,2 kp | 63,3 kp | 65,3 kp |
| α = 90° | 60,0 kp | 60,0 kp | 60,0 kp |
Conclusion: With 90° you would have a hoist, where the haulers can use their full 60kg as ballast. With 52° a hauler can use 54,7 kg of his 60 kg as counterweight. But using the rope roll a hauler is also pulling the stone at the rope, so in addition to his weight he also is using his strength (traction force).
 Calculating the required numbers of haulers with and without using the
rope roll
Calculating the required numbers of haulers with and without using the
rope roll
Egyptologists calculate that ramps of a gradient of 8 to 12° can
be managed by hauling teams. Our calculations (below) show, that slopes
of more than 5° already need large hauling teams and a slope of 10°
needs over 400 men! But with a pair of rope rolls installed directly on
the flank of the pyramid, an angle of inclination of 52° is no problem
at all and you only need 46 haulers!
![]() Löhner's rope roll
Löhner's rope roll
CHART 4 (figures [1] page 80)
* Number of men in a team: there are two groups walking down to the left and right side of the track. Furthermore there are always 2 men pulling side by side at the rope.
Construction ramps: Considering that you work on a very
narrow ramp, the hauling team should not be too large in numbers. A 50
men-team seems to be realistic and manageable. Anything larger certainly
poses problems, specially considering the length of the whole contraption
of sledge plus hauling teams. Most ramp theories don't consider these
facts and suggest ramps that are definitely too narrow or too steep.
![]() Theories of pyramid ramp systems disproved
Theories of pyramid ramp systems disproved
![]() Ramp models described in details
Ramp models described in details
 For checking purposes: increasing the coefficient of friction
For checking purposes: increasing the coefficient of friction
If we increase the coefficient of friction (= worse values) our calculations show that the 52° inclination of the pyramid face still can be managed. Using a coefficient of static friction μz of 0,1, a value that we are sure the Egyptians could achieve - we get a hauling team of 51 men instead of one of 46 men. This signifies, that lowering the coefficient of friction from 0,04 to 0,1 (= +150%) we will only need 5 men more (= +11 %).
2781 kp : 54,7 kp ≈ 51 haulers (2781 kp see chart 1, column 5 / 54,7 kp see chart 3, column 1)
Using the rope roll is already worth while on a moderate inclination of 5° (see chart 4) and inclinations of 10° or more virtually can not be managed without using rope rolls. |
 For checking purposes: increasing the force exerted by each hauler
For checking purposes: increasing the force exerted by each hauler
We calculate again, but with better values for the force exterted by each hauler. Instead of 12kp we use 15kp per person.
We use the same numbers as a well known American archeologist, Mark Lehner [6]. On level surface he assumes, that a 2.5 tons block could be pulled by 7.5 men. If we use the same coefficients of friction as before for our calculations, then we get a force of 15kp per hauler (chart 5, second column). To calculate these kind of numbers, Mark Lehner had to use a coefficient of static friction μo = 0.25 (chart 2, 2nd column).
Because Mark Lehner mentions in his text the well known frieze from the tomb of Djehutiotep at Deir El Bersheh, where 172 men haul a statue weighting about 60 tons, we also calculate the coefficient of friction μs and get 0,043 - on this page we did all our calculations with μs= 0,04 (172 x 15kp = 2580kp / 2580 : 60'000 = 0,043). More information.
Mark Lehner thinks, that with an angle of inclination of 6° a total of 20 men could haul the same 2.5 tons block, and cover a 333m-distance in 19 minutes. Our calculations on the contrary already show, that with an inclination of 5° you need already 36.5 haulers (chart 2, 2nd column for 15kp). Mark Lehner has, like a lot of other theorists, definitely undervalued the additional force, that is necessary, if you haul on an inclined plane!
On a 5° incline, even with a higher tractive force of 12kp instead of 15kp, you still need less haulers when using Löhner's rope rolls than without using them - we calculate only 23 instead of 36 men!
 Conclusions
Conclusions
Thanks to the rope roll the transport of a 2.5 tons stone block can be accomplished on the 52° flank of the pyramid with only 46 men. |
For transporting materials on a slope with an angle of inclination of
5° or more it is expedient to use Löhner's rope roll. This means
that the rope roll can also be used for transporting stones from the harbor
to the building yard close to the pyramid, while building the causeway
and for the transports from the quarries located on the Giza plateau to
the pyramid. The rope roll also is a useful resource in the quarries of
Aswan and can be used to load the granite stones onto the barges.
![]() Quarrying stones for the pyramid
Quarrying stones for the pyramid
![]() Shipping the stone blocks down the Nile to
Giza
Shipping the stone blocks down the Nile to
Giza
![]() Transporting the stone blocks using a sledge
on tracks
Transporting the stone blocks using a sledge
on tracks
![]() Löhner's rope roll
Löhner's rope roll
 Lifting the granite blocks with a heavy duty track system with counter
weights
Lifting the granite blocks with a heavy duty track system with counter
weights
Can this method also be used for hauling the 40 to 50 tons granite blocks
required for the King's chamber up the pyramid? Yes - using counterweight
stones and larger hauling teams. We use 8 large stones (5.6 tons each)
as counterweights and calculate, that the difference in weight is distributed
among 2 hauling teams. So the difference is, depending on the size of
the granite beam, from 3.2 to 7.2 tons (48-52t minus 44.8t). This works
out to 1.6 to 3.6 tons for each of the two hauling teams to the left and
right of the main track system. Our calculations show, that we need between
32 and 64 haulers per team.
![]() Transporting the large granite blocks
up the pyramid
Transporting the large granite blocks
up the pyramid
CHART 6 - hauling different weights (using the rope roll)
 Sources
Sources
[1] H. Illig and F. Löhner
Der Bau der Cheops-Pyramide pages 75 sqq. Calculations Dr. H.
Illig and Prof. Dr. Dipl. H.U. Niemitz
[2] Karl-Heinrich Grote, Jörg Feldhusen, Dubbel Taschenbuch für
den Maschinenbau
[3] G. Goyon Die Cheops-Pyramide
[4] Wikipedia Coefficient
of Friction / Stiction
/ Static
Friction / Inclined
plane
[5] D. Arnold Building in Egypt:
The stone blocks of the pyramid of Khufu were very large in the lower
layers (1m x 2.5m and 1-1.5m high, 6.5 - 10 tons) For the layers higher
up it was easier to transport smaller stone (1m x 1m and 0.5m high, 1.3
tons). For calculations most Egyptologists use 2.5 tons for the weight
of an average stone block.
[6] M. Lehner The Complete Pyramids
of Egypt page 225
Remarks: Translating this physics text from German into English was very challenging. Please excuse any mistakes I made.
| Copyright 2006: |
Franz Löhner www.cheops-pyramide.ch | |
| Concept and Design, English Texts: |
Teresa (Zubi) Zuberbühler www.starfish.ch |